11865. Метро в Баку

Метрополитен Баку – один из старейших и самых уникальных в регионе. Первая линия была открыта в 1967 году, и сегодня сеть охватывает десятки станций, среди которых известные, как "28 мая", "Ичери Шехер", "Низами" и другие. Особенностью бакинского метро являются глубокие станции, украшенные мозаикой, и наличие пересадочных узлов. В последние годы активно обсуждается создание кольцевой линии, которая бы соединила центральные и периферийные районы города.

В рамках проекта модернизации столичной подземки была разработана абстрактная модель схемы метро, включающая n станций и n тоннелей между ними. Каждый тоннель соединяет ровно две станции и не пересекает другие. При этом из любой станции можно добраться до любой другой, перемещаясь по тоннелям. Все тоннели работают в обоих направлениях, и между каждой парой станций не более одного прямого соединения.

Бакинские математики доказали теорему: в любой подобной схеме метро существует ровно один цикл. То есть можно найти кольцевую линию – маршрут, проходящий через ряд станций, в котором любые две соседние соединены тоннелем, и ни одна станция не встречается более одного раза.

Это открытие вызвало настоящий бум в городе: жители начали измерять расстояния своих станций до кольцевой. Один говорил: “я живу на расстоянии трёх станций от кольца”, другой – “всего одной”. Даже появились мобильные приложения, которые рассчитывают расстояние станции от кольцевой линии (конечно, с платной подпиской).

В целях контроля ситуации бакинское метрополитенное управление поручило вам разработать программу, которая по заданной схеме метро вычислит для каждой станции минимальное количество переходов, необходимое, чтобы попасть на кольцевую линию. Для станций, входящих в кольцо, расстояние считается равным нулю.

Вход. В первой строке задано целое число n (3 ≤ n ≤ 3000) – количество станций в схеме метро (оно же совпадает с количеством переездов). Далее следуют n строк, каждая из которых описывает один переезд. В каждой строке записана пара целых чисел x_i, y_i (1 ≤ x_i, y_i ≤ n), обозначающая наличие переезда между станциями x_i и y_i.

Станции пронумерованы от 1 до n в произвольном порядке.

Гарантируется, что x_i ≠ y_i, между каждой парой станций не более одного переезда, и переезды можно использовать в обе стороны. Также гарантируется, что схема метро является классической – то есть связной и содержащей ровно один цикл.

Выход. Выведите n чисел: i-е число должно быть равно расстоянию от i-й станции до кольцевой линии. Для станций, находящихся на кольцевой, выведите 0.

Пример входа 1	Пример выхода 1
5 1 2 1 4 5 3 5 2 3 4	0 0 0 0 0
Пример входа 2	Пример выхода 2
6 1 2 2 3 2 5 3 5 3 4 6 4	1 0 0 1 0 2

РЕШЕНИЕ

поиск в ширину

Анализ алгоритма

Дан связный неориентированный граф из n вершин и n рёбер. Граф содержит ровно один цикл. Для каждой вершины требуется определить расстояние до ближайшей вершины, лежащей на цикле. Если вершина уже входит в цикл, расстояние считается равным 0.

Граф можно представить как единственный цикл, к которому прикреплены висячие деревья. Чтобы найти вершины, входящие в цикл, используем метод пошагового удаления листьев (вершин степени 1):

· Пока в графе есть вершины степени 1, удаляем их.

· Когда таких вершин больше не останется, в графе останутся только вершины, образующие цикл.

Этот процесс напоминает обратную топологическую сортировку: мы последовательно удаляем листья, пока не останутся только “внутренние” вершины – именно они и составляют цикл.

Далее запускаем поиск в ширину одновременно из всех вершин, входящих в цикл. Таким образом для каждой оставшейся вершины определяем минимальное количество шагов (переходов) до ближайшей вершины кольца.

Пример

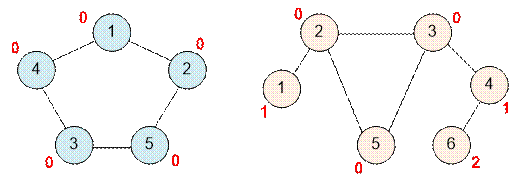
В первом примере все вершины входят в один цикл, поэтому расстояние для каждой из них равно 0.

Во втором примере цикл образуют вершины 2, 3 и 5, а остальные вершины находятся на некотором расстоянии от него.

Реализация алгоритма

Объявим список смежности графа g, а также вспомогательные массивы:

· used – хранит информацию о состоянии вершин (удалена или входит в цикл);

· dist – содержит расстояние от каждой вершины до ближайшей вершины, находящейся на цикле;

· deg – хранит степень каждой вершины (число смежных вершин).

vector<vector<int> > g;

vector<int> used, dist, deg;

queue<int> q;

Читаем входные данные. Строим граф.

scanf("%d", &n);

g.resize(n + 1);

for (i = 0; i < n; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Вычисляем степени всех вершин. Вершины со степенью 1 добавляем в очередь q.

used.resize(n + 1, 0);

deg.resize(n + 1, 0);

for (i = 1; i <= n; i++)

{

deg[i] = g[i].size();

if (deg[i] == 1)

{

q.push(i);

used[i] = 1;

}

}

Далее запускаем поиск в ширину, начиная одновременно из всех вершин степени 1. В процессе обхода будут отмечены как посещённые те вершины, которые не принадлежат циклу – они постепенно “обрезаются” от графа, как листья.

while (!q.empty())

{

int v = q.front(); q.pop();

for (int to : g[v])

if (used[to] == 0)

{

deg[to]--;

Поиск в ширину продолжаем из вершины to только в том случае, если её степень становится равной 1 – то есть она превращается в новый лист.

if (deg[to] == 1)

{

q.push(to);

used[to] = 1;

}

}

}

На данный момент значение used[i] = 0 только если вершина i принадлежит циклу. Теперь все вершины, входящие в цикл, заносим в очередь q. Также инициализируем массив dist, который будет хранить кратчайшие расстояния от каждой вершины до ближайшей вершины цикла.

dist = vector<int>(n + 1, -1);

q = queue<int>();

for (i = 1; i <= n; i++)

if (used[i] == 0)

{

q.push(i);

dist[i] = 0;

}

Запускаем поиск в ширину, начиная с вершин, уже находящихся в очереди q – это вершины, входящие в цикл. В ходе обхода вычисляем расстояния от цикла до всех остальных вершин графа.

while (!q.empty())

{

int v = q.front(); q.pop();

for (int to : g[v])

if (dist[to] == -1)

{

q.push(to);

dist[to] = dist[v] + 1;

}

}

Выводим ответ.

for (i = 1; i <= n; i++)

printf("%d ", dist[i]);

printf("\n");